Effizienter Schaltungsentwurf für zeitdiskrete analoge Schaltungen
Getaktete analoge Schaltungen werden in der modernen integrierten Schaltungstechnik sehr häufig eingesetzt. Es gibt inhärent zeitdiskrete Schaltungen und solche, die eine eigentlich kontinuierliche Größe (wie Spannung) durch Abtastung, getaktete Ladevorgänge oder Mittelung in eine zeitdiskrete umwandeln.
Analog-Digital-Umsetzer (ADCs) sind ein Beispiel für zeitdiskrete Schaltungen, die die kontinuierliche Größe Spannung durch Abtastung in eine zeitdiskrete verwandeln. Gleichspannungswandler (DC-DC Converter) bilden eine kontinuierliche Spannung wieder auf eine kontinuierliche Spannung ab, aber der Umsetzungsprozess benützt einen getakteten Vorgang. Diese Wandler benützen daher eine zeitdiskrete Regelschleife. Chopper Verstärker bilden eine Spannungsdifferenz durch eine getaktete Mittelung auf eine Spannung ab. Phasenregelschleifen (PLLs) erzeugen Frequenzen und messen den zeitlichen Abstand zwischen 2 Flanken. Damit sind sie inhärent zeitdiskrete Schaltungen. Sowohl Frequenz als auch Flankenabstand sind zeitdiskrete Größen. Ihre Behandlung als Kontinuum erzeugt Probleme bei der Modellierung [1-3], die vergleichbar sind mit der Beschreibung eines Fußgängers mit Handy, ohne zu berücksichtigen, dass dieser nicht immer auf den Weg schaut.
So kann ein Fußgänger der nur alle 2s von seinem Handy aufschaut auf keine Vorgänge im Sekundentakt reagieren.

Vergleichbar dazu nähert man bei einer kontinuierlichen Beschreibung eine Addition durch eine Integration an. Bei einer Addition tritt eine Verzögerung auf, da immer zu bestimmten Zeitpunkten addiert wird. Dies wird vernachlässigt.
Eine Integration verursacht 90° Phasendrehung. Nähert man sich mit der Frequenz der Ereignisse der Frequenz f_ref mit der die Addition ausgeführt wird, so bewirkt diese Verzögerung der „Integration“ immer mehr zusätzliche Phasendrehung. Bei f_ref/4 wird die Phase schon um 45° falsch eingeschätzt (siehe Bild unten).
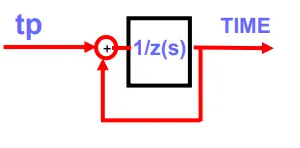
Für die meisten Systeme bedeutet das den Verlust der Stabilität
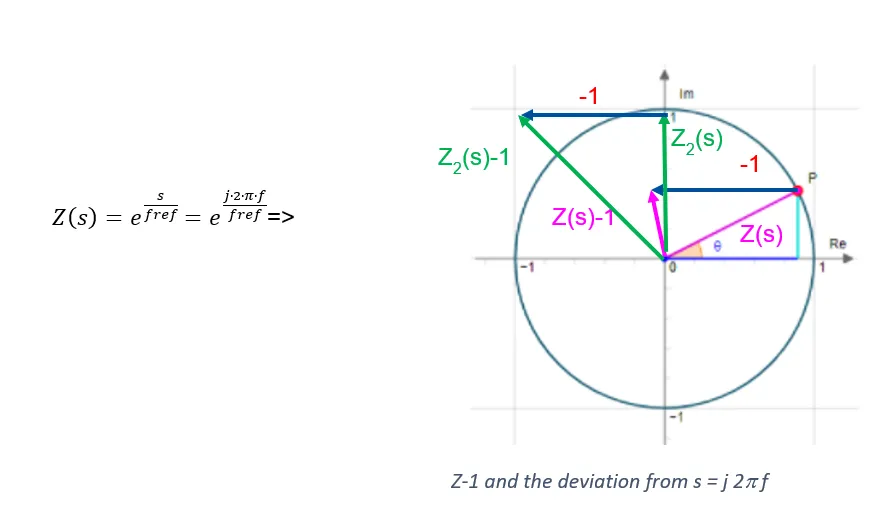
Obwohl PLLs gar keine kontinuierlichen Größen erzeugen oder messen, wird die Regelschleife als zeitkontinuierliches System modelliert. Dies führt dazu, dass Rauschübertragungsfunktionen nicht korrekt ermittelt werden können und deswegen auch im Schaltungsentwurf nicht benützt werden um die Anforderungen an die einzelnen Komponenten zu ermitteln, sondern nur um das prinzipielle Zusammenspiel zu erläutern.
Wenn eine getaktete Modellierung verwendet wird, dann wird sie aus der zeitkontinuierlichen Modellierung ableitet [4-7]. Damit schließt man systematisch Effekte die durch den Takt hervorgerufen werden aus. So haben kontinuierliche Schaltungen eine Durchlaufzeit von 0. Getaktete Systeme haben aber Durchlaufzeit von N Taktperioden. Mindestens jedoch von einer Taktperiode.
Diese Diskrepanz wird in modernen CMOS Prozessen immer problematischer, da die Taktfrequenzen für die analogen Schaltungen steigen.
Das aktuelle Vorgehen einzelne Komponenten zu verbessern ohne eine quantitative Vorhersage über das Potential der möglichen Verbesserung zu treffen ist vergleichbar wie in den 1950ern Fahrräder entwickelt wurden:
Man nahm ausreichend dicke Metallrohre, schweißte daraus einen Rahmen und montierte die beweglichen Teile. Dies funktionierte gut, das Fahrrad war nur unnötig schwer und man verbrauchte mehr Material als notwendig.
Später ging man dazu über ein Kräftediagram aufzustellen und konnte so ermitteln, wie dick die Rohre an welcher Stelle sein mussten. Dadurch konnte man sowohl Material einsparen und so das Fahrrad billiger anbieten, als es auch leichter machen.
Auf Schaltungen übertragen heißt das beispielsweise, dass man statt bekannte Schaltungen zu verändern, bekannte Prinzipien verstehen und erweitern könnte. Die Entkopplung eines Prinzips von einem Block ermöglicht ein viel tieferes Schaltungsverständnis. So findet die Integration der Frequenz zur Phase innerhalb einer PLL weder im PFD noch im VCO statt, sondern geschieht vielmehr dadurch, dass man die Phase anstatt der Frequenz betrachtet. Das ist vergleichbar, ob man bei einer Autofahrt die zurückgelegte Entfernung statt der Geschwindigkeit betrachtet. Der Blick auf die Funktionsweise ermöglicht Parallelen und Unterschiede zwischen Schaltungsgruppen zu analysieren und die Grenzen für gängige Daumenregeln zu erkennen. Die Optimierung bestimmter Komponenten könnte man unter eine Aufwand Nutzen Analyse für das Gesamtsystem stellen. Man könnte zeitdiskrete Schaltungen schneller und mit nicht so erfahrenen Designern entwickeln. Außerdem würden der Chipflächen und Leistungsverbrauch sinken.
Eine vertrauenswürdige Modellierung ermöglicht auch die schnelle Evaluierung von neuen Konzepten. Dies ist natürlich nicht auf PLLs beschränkt, sondern gilt für alle getakteten analogen Schaltungen. Statt kostenintensive empirische Experimente durchzuführen wird die Evaluierung schon im Modell möglich. So kann man beispielsweise schon im Modell erkennen, dass 2 Proportionalpfade die gleiche Wirkung wie einer haben, auch wenn sie zeitversetzt sind.
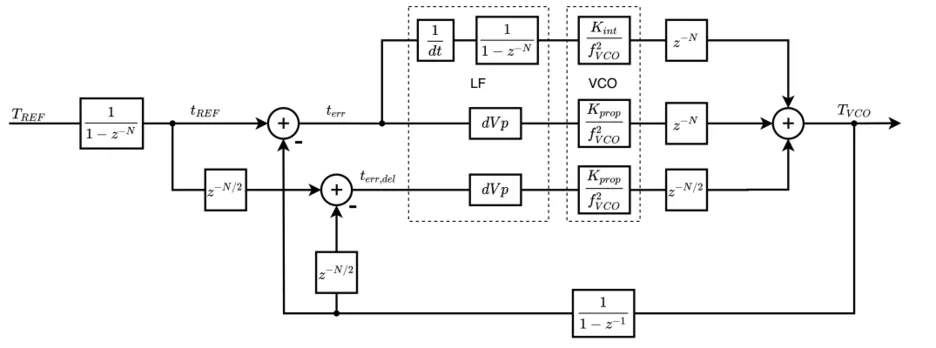
Ein allgemeingültiger Modellierungsansatz für die Schaltungskomponenten und das System einer PLL (und später auch weiterer der oben erwähnten getakteten Schaltungen) würde so ein besseres und tieferes Verständnis dieser Schaltungsklassen zum Zweck der Optimierung in der Anwendung aber auch in der Lehre zur Ausbildung zukünftiger Schaltungsentwickler ermöglichen. Nach dem Stand der Technik [2] wird das In-Band-Rauschen der PLL beispielsweise durch den Proportional- und den Integralweg erzeugt (Schleifenrauschen). Dies würde bedeuten, dass das Rauschen mit zunehmender PLL-Bandbreite schlechter werden sollte. Da die maximale Bandbreite jedoch durch die Referenztaktfrequenz bestimmt wird, ist es oft nicht möglich, die Bandbreite zu optimieren, um den PLL-Schleifenjitter an den VCO-Jitter anzupassen. Außerdem lässt sich vernünftig begründen, dass die Hauptquelle des PLL-In-Band-Rauschens der VCO und nicht die Schleife ist. Um dies zu beweisen, ist eine hohe Bandbreite erforderlich, und deshalb wurde eine PLL mit einer sehr hohen Referenzfrequenz von 3 GH abgegriffen, um einen PLL-Ausgangstakt von 6 GHz zu erzeugen. Dies ermöglicht es uns, die Bandbreite auf über 200 MHz zu erhöhen. Das In-Band-Rauschen der PLL nimmt bei einer so großen Bandbreite nicht zu, sondern eher ab. Es kann also bewiesen werden, dass der VCO die dominierende Rauschquelle des PLL-In-Band-Rauschens ist (siehe Bild unten).
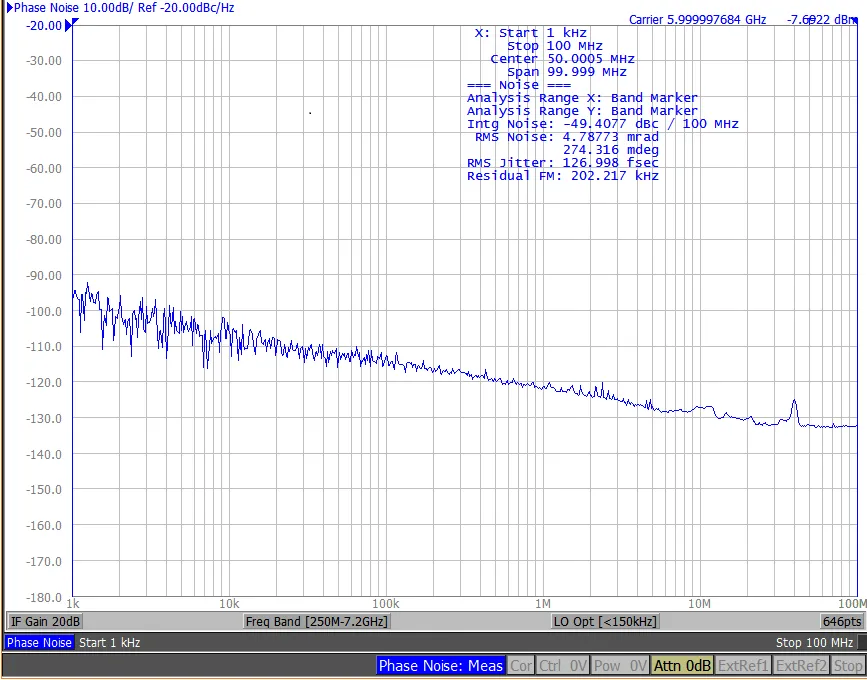
[1] D. Kim and S. Cho, "A hybrid PLL using low-power GRO-TDC for reduced in-band phase noise," IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 66, no. 2, pp. 232-236, 2018.
[2] X. Gao, E. A. Klumperink, P. F. Geraedts, and B. Nauta, "Jitter analysis and a benchmarking figure-of-merit for phase-locked loops," IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 56, no. 2, pp. 117-121, 2009.
[3] G. Urakawa, H. Kobayashi, J. Deguchi, and R. Fujimoto, "A Noise-Canceling Charge Pump for Area Efficient PLL Design," in 2020 IEEE International Symposium on Radio-Frequency Integration Technology (RFIT), 2020: IEEE, pp. 31-33.
[4] J. P. Hein and J. W. Scott, "z-domain model for discrete-time PLL's," IEEE transactions on Circuits and Systems, vol. 35, no. 11, pp. 1393-1400, 1988.
[5] B. Razavi, "zDomain Model for DiscreteTime PLL's," 1996.
[6] B. Razavi, Design of CMOS phase-locked loops: from circuit level to architecture level. Cambridge University Press, 2020.
[7] C.-H. Tsai, Z. Zong, F. Pepe, G. Mangraviti, J. Craninckx, and P. Wambacq, "Analysis of a 28-nm CMOS Fast-Lock Bang-Bang Digital PLL With 220-fs RMS Jitter for Millimeter-Wave Communication," IEEE Journal of Solid-State Circuits, vol. 55, no. 7, pp. 1854-1863, 2020.